正弦、余弦和正切
三个函数,一个概念。
直角三角形正弦、余弦和正切是 三角法 里的主要函数,它们是基于一个 直角三角形而建立的。
在探索这些函数之前,我们先给三角形的每条边一个名字:
"对边" 是在角 θ 的对面
"邻边" 是在角 θ 的旁边
"斜边" 是长的一边
邻边 是在角的旁边
对边 是在角的对面
正弦 (sine), 余弦 (cosine) 和 正切 (tangent) (英语符号简写为 sin, cos 和 tan) 是 直角三角形 边长的比:
对一个特定的角 θ 来说,不论三角形的大小,
这三个比是不变的
计算方法:
用一条边的长度除以另一条边的长度
例子: 35°的正弦是多少?

用这三角形来算 (长度精确到一位小数):
sin(35°) = 对边 / 斜边
好的计算器都会有 sin, cos 和 tan 的键,方便计算。你只需输入角度然后按键。
可是你还是要记得它们的意思!
用图来显示:
怎样去记住? 想想,用这个怪怪的英文单词 "Sohcahtoa"!
像这样:
Soh...
Sine = Opposite (对边) / Hypotenuse (斜边)
...cah...
Cosine = Adjacent (邻边) / Hypotenuse (斜边)
...toa
Tangent = Opposite (对边) / Adjacent (邻边)
去这页 sohcahtoa 了解更多。。。。。。 记住它,考试时会有用!
试试看!试 试 看! 移动鼠标,不同的角(以弧度或度数为单位)对 正弦、余弦和正切的影响。
在这个动画里,斜边是 1,圆形是 单位圆。
请注意邻边和对边可以是负值,导致正弦、余弦和正切的值也可正可负。
例子例子: 30° 的正弦、余弦和正切是什么?
传统的 30° 三角形的 斜边为 2、对边为 1 和邻边为 √3:
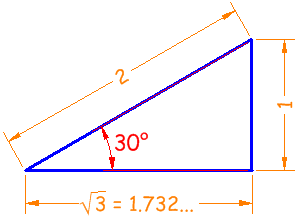
知道边长,便可以计算函数的值:
正弦 余弦 正切
(用计算器来检查答案!)
例子: 45° 的正弦、余弦和正切是什么?
传统的 45° 三角形有两条边长为 1,斜边为 √2:
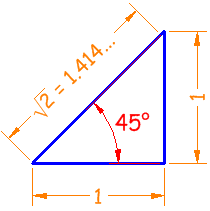
正弦 余弦 正切
为什么这些函数重要?
因为当我们知道边长时,我们可以用它们来计算角度
同时,当我们知道角度时,我们也可以用它们来计算边长
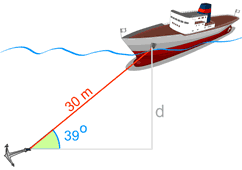
我们知道:
电缆与海底成 39° 的角
电缆长度为 30 米。
我们求 "d" (垂直向下距离)。
这样开始:
sin 39° = 对边/斜边
sin 39° = d/30
两边互换:
d/30 = sin 39°
用计算器来求 sin 39°:
d/30 = 0.6293…
两边乘以 30:
d = 0.6293… x 30
d = 18.88 计算结果保留两位小数。
深度 "d" 是 18.88 m
习题试试这个 纸上习题。计算 从 0° 到 360° 所有角的正弦,然后画个图表。这会帮助你了解这个相当简单的函数。
你也可以去 正弦、余弦和正切的图形看看。
不常见的函数还有三个函数也是把一边除以另一边,不过我们不常用它们。
它们等于 1 除以 余弦、1 除以 正弦 和 1 除以 正切:
正割 函数:
sec(θ) = 斜边 / 邻边 (=1/cos)余割 函数:
csc(θ) = 斜边 / 对边 (=1/sin)余切 函数:
cot(θ) = 邻边 / 对边 (=1/tan)